Paper Citation: Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains
Problem
Fully connected MLPs struggle to capture high frequency details in low dimensional problems. In this example the network is given (x, y) coordinates and learns the RGB values of the image. However, since NNs learn smooth functions, a network struggles to represent both high level and the finer details.

Solution
With standard untransformed features, the input space essentially has a single frequency. The network must learn details at some relatively fixed level of granularity. By transforming the inputs at multiple frequencies, we can instead encourage the networks to learn at different levels of granularity (different kernel widths). It will capture large scale patterns at low frequency, and details like the fox’s fur at higher frequencies. The image below shows how this works. Instead of just a single frequency, we use many different frequencies. The B values are just sampled before training (and kept fixed) from a zero-centered Gaussian distribution.
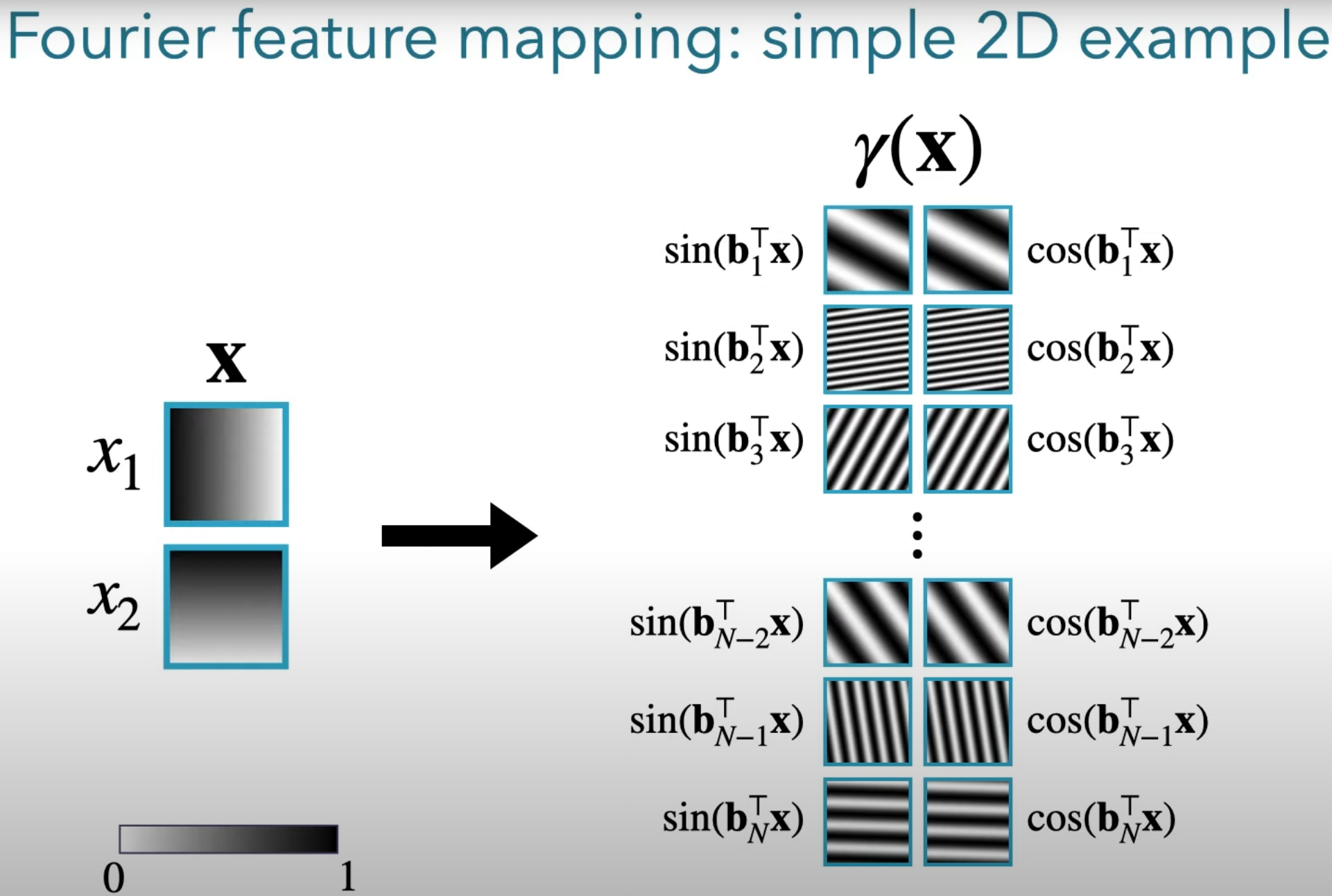 If you aren’t familiar with Fourier transforms, the intuition behind using both sin(x) and cos(x) is simple. If you only use sin(x), then you’ll have two locations of x where the transformed feature is identical, so by including cos(x) we preserve the information in the coordinates.
If you aren’t familiar with Fourier transforms, the intuition behind using both sin(x) and cos(x) is simple. If you only use sin(x), then you’ll have two locations of x where the transformed feature is identical, so by including cos(x) we preserve the information in the coordinates.
In essence, this technique enables the network to perform interpolation at different scales, which means it can fully represent the image.
Paper video: